FX Series Programmable Controlers Applied Instructions 5
5-105
Configuring the PID loop
The PID loop can be confi
g
ured to offer variations on PID control. These are as follows:
It should be noted that in all situations there must be a proportional or ‘P’ element to the loop.
P - proportional change
When a proportional factor is applied, it calculates the difference between the Current Error
Value, EV
n
, and the Previous Error Value, EV
n-1
. The Proportional Chan
g
e is based upon how
fast the Process Value is movin
g
closer to (or further awa
y
from) the Set Point Value NOT
upon the actual difference between the PV
nf
and SV.
Note: Other PID s
y
stems mi
g
ht operate usin
g
an equation that calculates the Proportional
chan
g
e based upon the size of the Current Error Value onl
y
.
I - integral change
Once a proportional chan
g
e has been applied to an error situation, ‘fine tunin
g
’ the correction
can be performed with the I or inte
g
ral element.
Initiall
y
onl
y
a small chan
g
e is applied but as time increases and the error is not corrected the
inte
g
ral effect is increased. It is important to note how T
I
actuall
y
effects how fast the total
inte
g
ral correction is applied. The smaller T
I
is, the bi
gg
er effect the inte
g
ral will have.
Note: The T
I
value is set in data re
g
ister S
3
+4. Settin
g
zero for this variable disables the
Inte
g
ral effect.
The Derivative Change
The derivative function supplements the effects caused b
y
the proportional response. The
derivative effect is the result of a calculation involvin
g
elements T
D
, T
S
, and the calculated
error. This causes the derivative to initiall
y
output a lar
g
e corrective action which dissipates
rapidl
y
over time. The speed of this dissipation can be controlled b
y
the value T
D
: If the value
of T
D
is small then the effect of appl
y
in
g
derivative control is increased.
Because the initial effect of the derivative can be quite severe there is a ‘softenin
g
’ effect which
can be applied throu
g
h the use of
K
D
, the derivative
g
ain. The action of
K
D
could be
considered as a filter allowin
g
the derivative response to be scaled between 0 and 100%.
The phenomenon of chasin
g
, or overcorrectin
g
both too hi
g
h and too low, is most often
associated with the Derivative portion of the equation because of the lar
g
e initial correction
factor.
Note: The T
D
value is set in Data re
g
ister S
3
+6. Settin
g
zero for this variable disables the
Derivative effect.
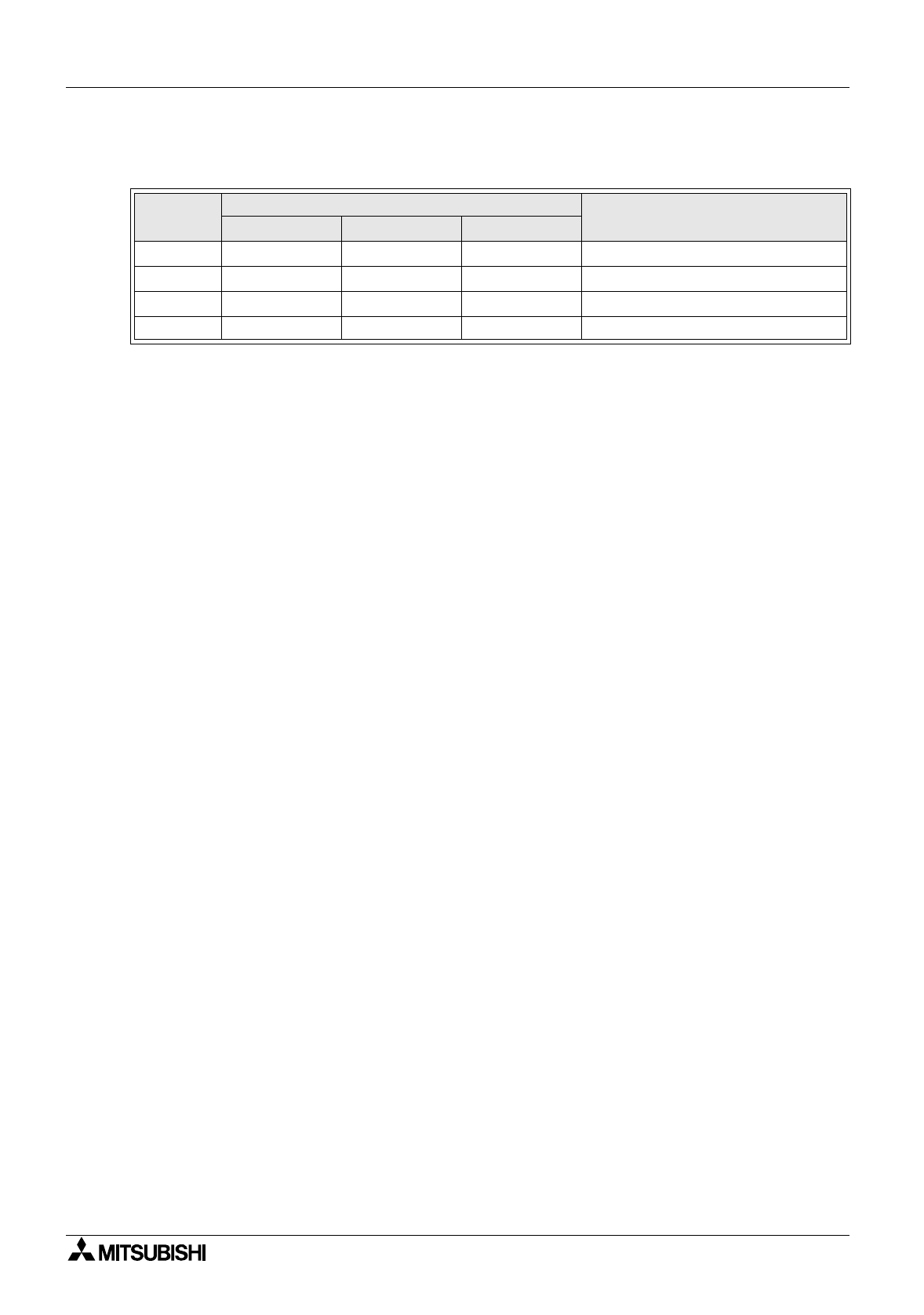
Control
method
Selection via setup registers
Description
S
3
+3 (
K
P
) S
3
+ 4 (
T
I
) S
3
+ 6
(T
D
)
P User value Set to 0 (zero) Set to 0 (zero) Proportional effect onl
y
PI User value User value Set to 0 (zero) Proportional and inte
g
ral effect
PD User value Set to 0 (zero) User value Proportional and derivative effect
PID User value User value User value Full PID


















