HPM-2002-OBEVacuum Gauge Page 28 of 39
4.3. Pirani Sensor
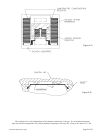
Figure 4.3a shows a thin metal film resistive element on a one micron thick Si
3
N
4
continuous membrane
surrounded by a thin film reference resistor on a Si substrate. The membrane is heated to a constant 8 °C above
ambient temperature that is monitored by the substrate resistor. The membrane resistor is approximately 60 Ω
and a constant substrate to membrane resistance ratio is maintained. Figure 4.3b shows the Pirani die in cross
section. A parallel Si lid is eutectically bonded to the Au pads and sits 5 microns above the membrane. As
shown, this dimension gives a Knudsen number of greater than 0.01 up to atmospheric pressure, which ensures
a molecular flow component. At 10 Torr the region above the membrane is totally in the molecular flow regime
and thus provides a relatively linear output verses pressure overlapping the linear output versus pressure of the
piezo.
The measurement technique is to produce an output signal that is proportional to the power supplied to the
heated resistor by using the product of the current and voltage. This rejects errors introduced by resistance
changes since the sensor resistance is no longer part of the power equation.
A signal proportional to the power is obtained by multiplying the voltage across the heated sensor and the
voltage impressed by the direct current across a constant series resistance. The power supplied to the sensor
resistor must equal the heat dissipated (E
t
). The three main heat loss routes from the heated sensor are thermal
conduction through the silicon nitride membrane to the silicon substrate (E
s
) radiation losses (E
r
) and thermal
conduction through the gas to the silicon substrate (E
g
); thus, as shown in Figure 4.3b,
E
t
= E
s
+ E
r
+ E
g
The first term, E
s
, is dependent on the thermal conductivity of the silicon nitride (K), the temperature
difference (∆T) between the heater and silicon substrate and geometric factors (A
M
& L). E
S
is given by
E
s
= (K ∆T A
m
)/L
A
m
is the membrane cross sectional area through which the heat transfer occurs. This is, approximately, the
outer circumference of the membrane multiplied by the membrane thickness. L is the distance from the edge of
(Rs) the heated sensor resistor to the silicon substrate.
For any particular sensor, all of the factors, except ∆T, are constants dependent on its construction. The ∆T
is held constant by the control circuit. The thermal loss through the silicon nitride will be a constant value
independent of the thermal conductivity and pressure of the gas.
Radiation is another source of thermal losses. It can be determined from
E
r
= σε(T
h
4
-T
a
4
)A
s
where
σ = Stefan-Boltzmann radiation constant
ε = thermal emissivity of the silicon nitride membrane
A
S
= surface area of the heated portion of the membrane
T
h
= temperature of R
s
T
a
= ambient temperature