Example PID Algorithm Listings 493Appendix G
PIDB Algorithm
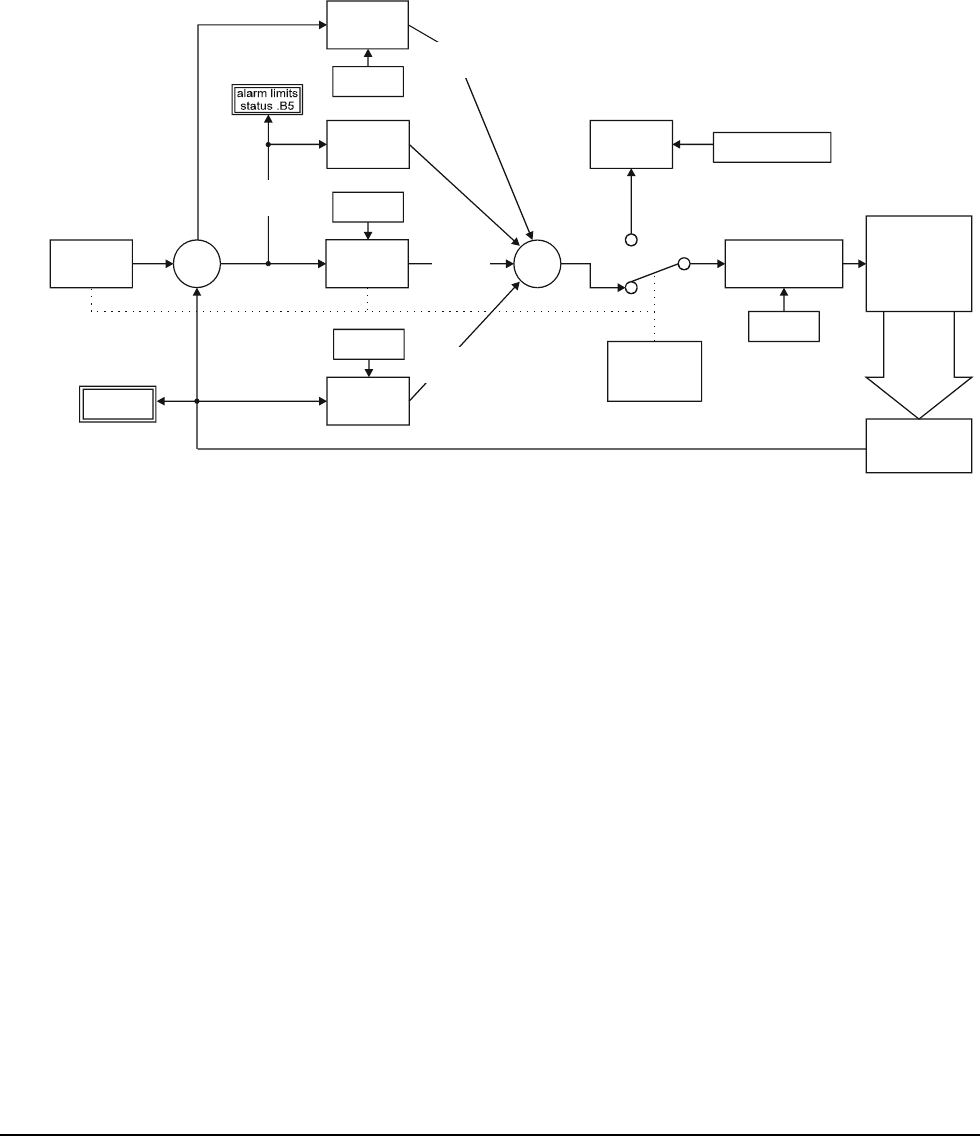
Figure G-2 shows the block diagram of a more advanced algorithm that is
favored in process control because of the flexibility allowed by its two
differential terms. The "D" differential term is driven by changes in the
process input measurement. The "SD" differential term is driven by changes
in the setpoint variable value.
Clipping Limits The PIDB algorithm provides clipping limits for its I, D, SD terms and the
value sent to <outp_chan>. Values for these terms are not allowed to range
outside of the set limits. The variables that control clipping are:
I term limits; I_max and I_min
D term limits; D_max and D_min
SD term limits; SD_max and SD_min
<outp_chan> limits; Out_max and Out_min
Alarm Limits The PIDB algorithm provides Alarm Limits for the process variable PV
and the Error term variable Error. If these limits are reached, the algorithm
sets the value of <alarm_chan> true and generates a VXIbus interrupt.
The variables that control alarm limits are:
Process Variable (from <inp_chan>); PV_max and PV_min
Error term alarm limits; Error_max and Error_min
The max and min limits for clipping and alarms are set to 9.9E+37 and
-9.9E+37 respectively when the algorithm is defined. This effectively turns
the limits off until the values are changed with the ALG:SCALAR and
ALG:UPDATE commands as described in "Pre-setting PID Variables and
Coefficients" later in this section.
Setpoint
Variable
+
+
+
+
+
-
<outp_chan>
channel
<inp_chan>
channel
process
P_factor
Variable
Man_state
Variable
status .B4
Man_out
Variable
SD_factor
Variable
D_factor
Variable
I_factor
Variable
Σ
Σ
I_out
variable
D_out
variable
Error
variable
clip limits
status .B0
clip limits
status .B3
clip limits
status .B1
slew rate limited by
Man_inc variable
clip limits
status .B2
alarm limits
status .B6
SD_out
variable
manual
auto
Figure G-2. The Advanced Algorithm "PIDB"


















