AX2500/2850 Motor Controller User’s Manual 121
Control Loop Description
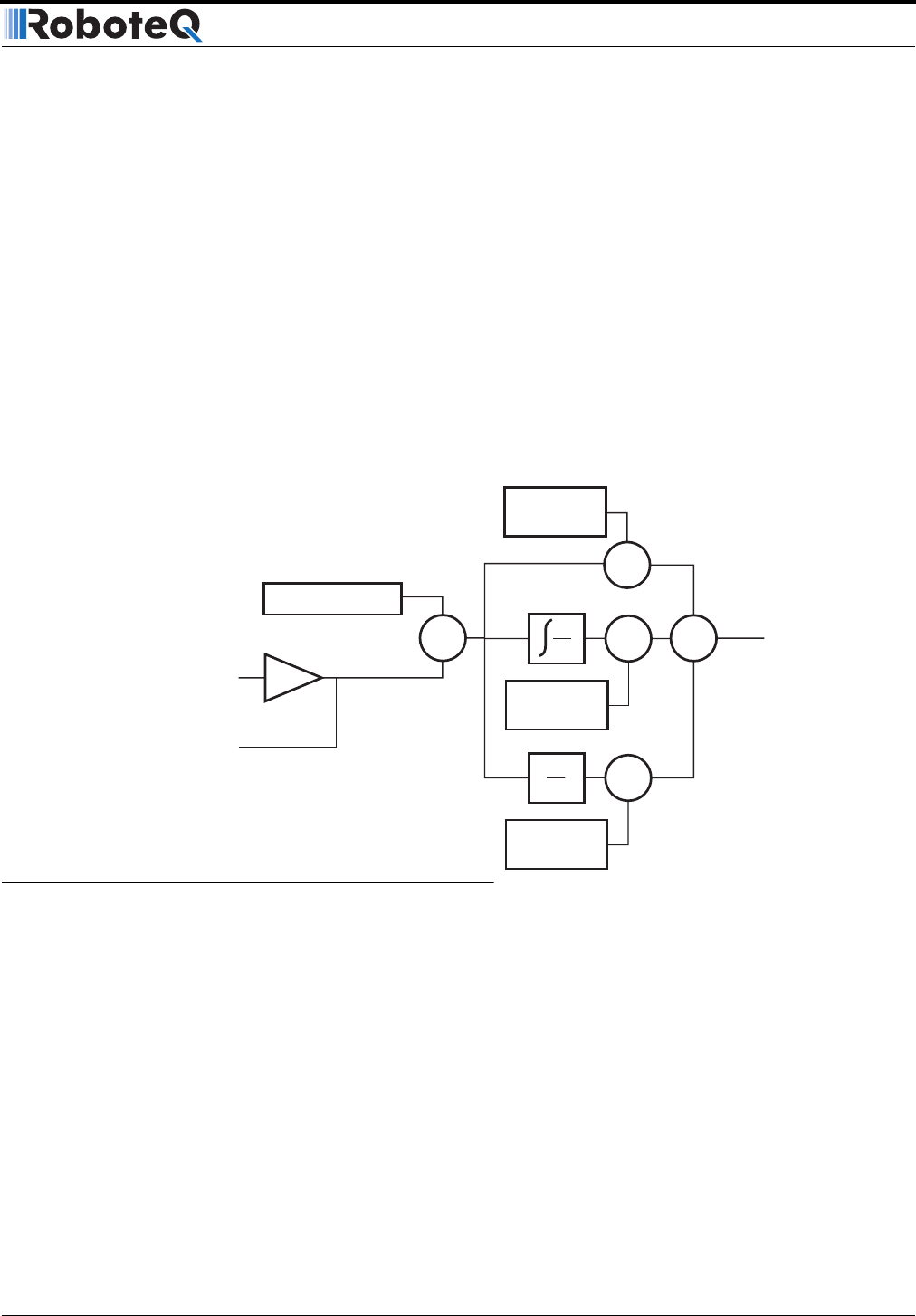
Figure 73 shows a representation of the PID algorithm. Every 16 milliseconds, the control-
ler measures the actual motor position and substracts it from the desired position to com-
pute the position error.
The resulting error value is then multiplied by a user selectable Proportional Gain. The
resulting value becomes one of the components used to command the motor. The effect
of this part of the algorithm is to apply power to the motor that is proportional with the dis-
tance between the current and desired positions: when far apart, high power is applied,
with the power being gradually reduced and stopped as the motor moves to the final posi-
tion. The Proportional feedback is the most important component of the PID in Position
mode.
A higher Proportional Gain will cause the algorithm to apply a higher level of power for a
given measured error thus making the motor move quicker. However, because of inertia, a
faster moving motor will have more difficulty stopping when it reaches its desired position.
It will therefore overshoot and possibly oscillate around that end position.
The Differential component of the algorithm computes the changes to the error from one
16 ms time period to the next. This change will be a relatively large number every time an
abrupt change occurs on the desired position value or the measured position value. The
value of that change is then multiplied by a user selectable Differential Gain and added to
the output. The effect of this part of the algorithm is to give a boost of extra power when
starting the motor due to changes to the desired position value. The differential component
will also greatly help dampen any overshoot and oscillation.
The Integral component of the algorithm perform a sum of the error over time. In the posi-
tion mode, this component helps the controller reach and maintain the exact desired posi-
tion when the error would otherwise be too small to energize the motor using the
Proportional component alone. Only a very small amount of Integral Gain is typically
required in this mode.
Desired Position
Differential
Gain
Proportional
Gain
E= Error
Output
Measured Position
Analog Position
Sensor
or
Optical Encoder
A/D
-
x
Σ
x
dE
dt
Integral
Gain
x
dE
dt
FIGURE 73. PID algorithm used in Position mode


















